
Let's remember that a fraction is a way of showing parts of a whole, whether that whole consists of objects or values. It involves splitting or dividing an object or value into equal parts and showing how many of those parts are being considered or used.
When you subtract fractions, the process is all about taking away one fraction from a whole to see what's left.
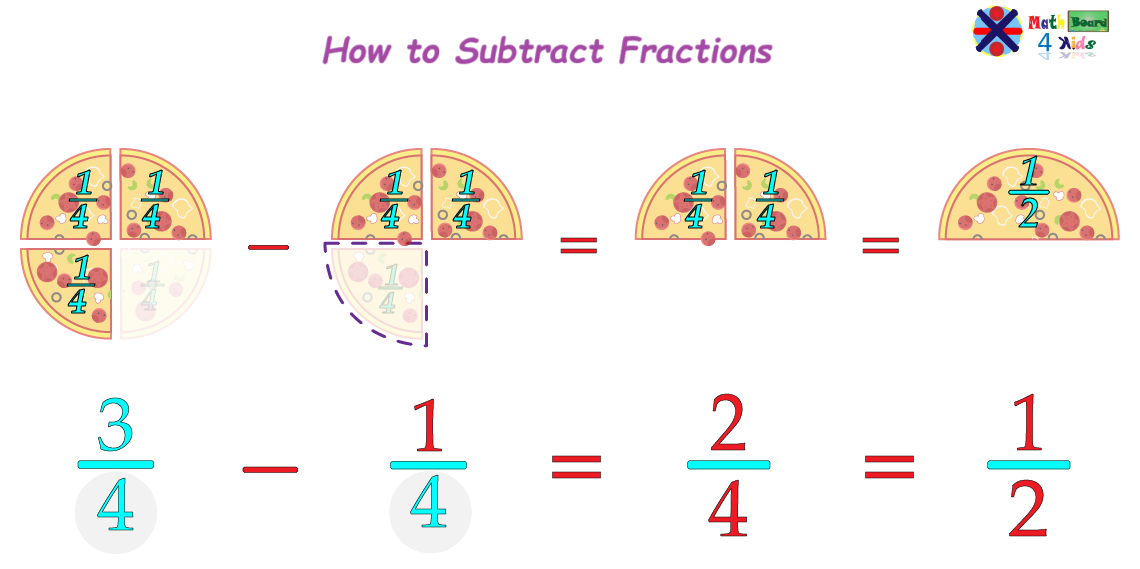
For the subtraction to work, we first need to make sure the fractions have the same, or a common denominator. This is where the idea of a common denominator becomes important.
A common denominator is a number that both denominators (the bottom numbers) of two or more fractions have in common. For example, ¾ - ¼.
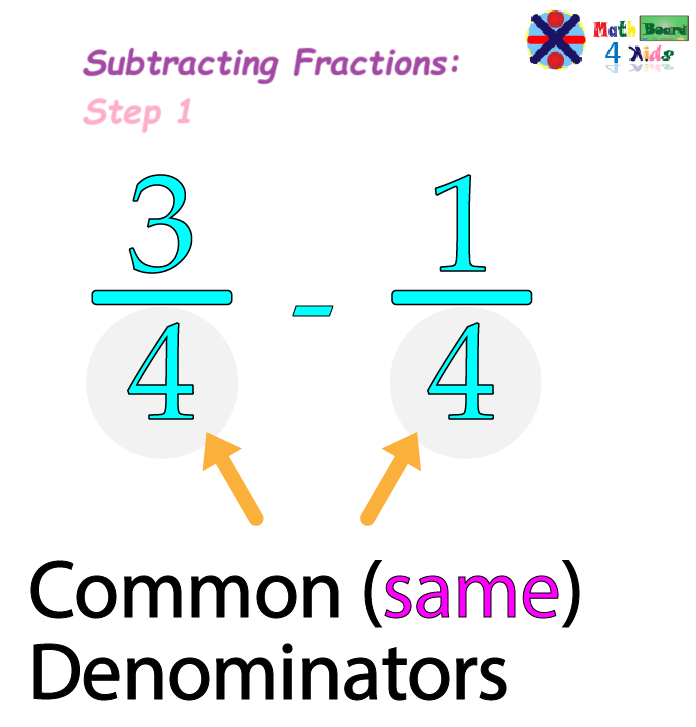
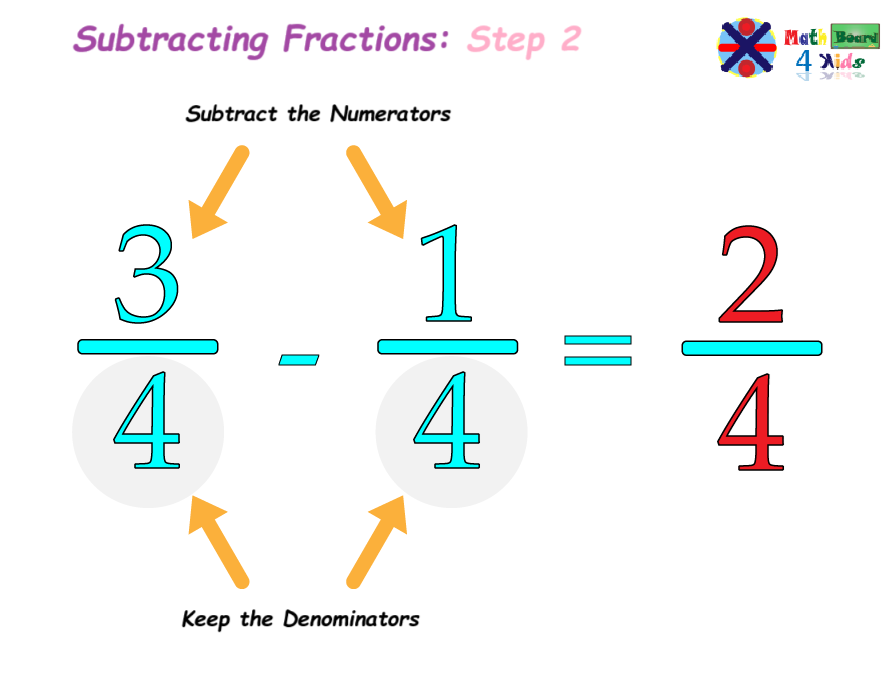
Since both fractions have the same denominator, we can simply subtract the numerators (the top numbers), and keep the denominators the same.
After subtracting the fractions, the next step is to check if the result can be simplified.
In order to simplify a fraction, we need to find the Greatest Common Factor (GCF), a number that helps make fractions simpler by reducing them to their smallest value.
The greatest common factor is the largest number that can evenly divide both the numerator and denominator of a fraction. For example, in the fraction 2/4, both the numerator and the denominator can be divided by 1 and 2.
Since 2 is the larger of these two numbers, we choose 2 as the greatest common factor and divide both the numerator and denominator by 2.
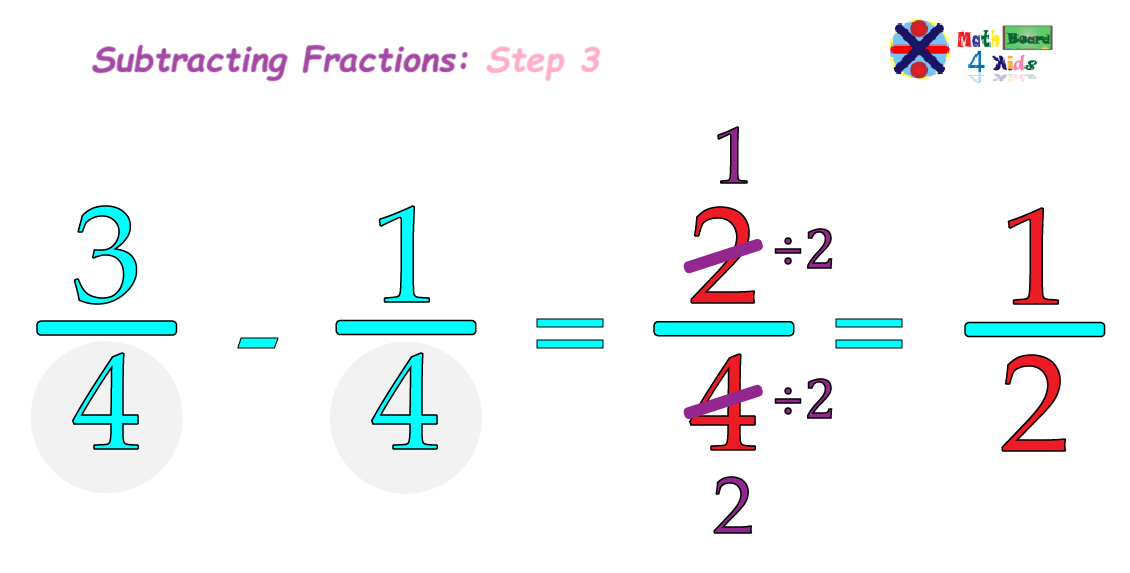
Unlike fractions are fractions with different denominators. In other words, the bottom numbers of the fractions are not the same.

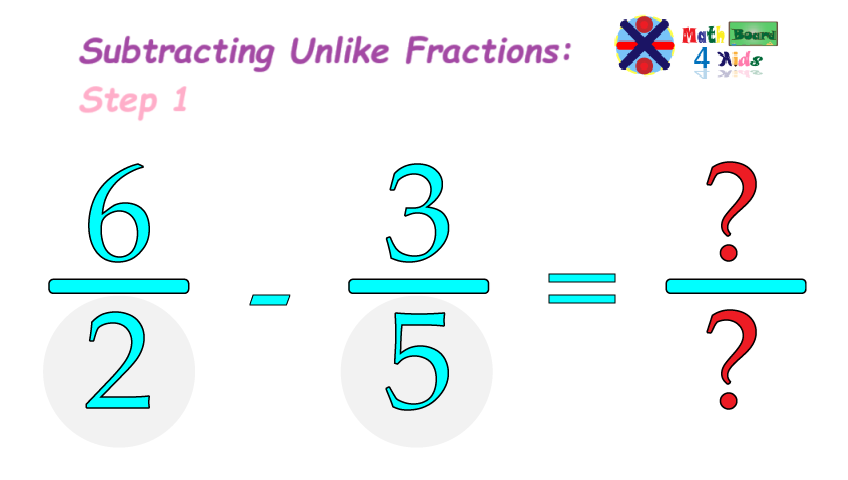
When adding or subtracting, if the fractions are unlike, we must find a common denominator before combining them.
We can find a common denominator by looking for the Least Common Denominator (LCD).
The Least Common Denominator (LCD) is the smallest number that both denominators can be used to divide evenly, without leaving any remainder. Let's learn how to find it!
To find the LCD easily, we need to list the multiples of each denominator — in this case, the multiples of 2 and 5. Then, identify the multiples both numbers have in common.

We've identified the multiples that both numbers share:
Multiples of 2
10, 20, etc.
Multiples of 5
10, 20, etc.
After listing the multiples that 2 and 5 have in common, we see that the smallest number that appears in both lists is 10, so 10 is the LCD.

Once we've found the LCD which is 10, we need to rewrite both fractions so that they have the same denominator.
In this case, to make the denominators equal, we multiply the first denominator (2) by 5, to reach the LCD (10), and then we multiply the and denominator (5) by 2 to reach the same LCD (10).
We also have to multiply the first numerator (6) by 5, and the second second numerator (3) by 2 to make both fractions equivalent.
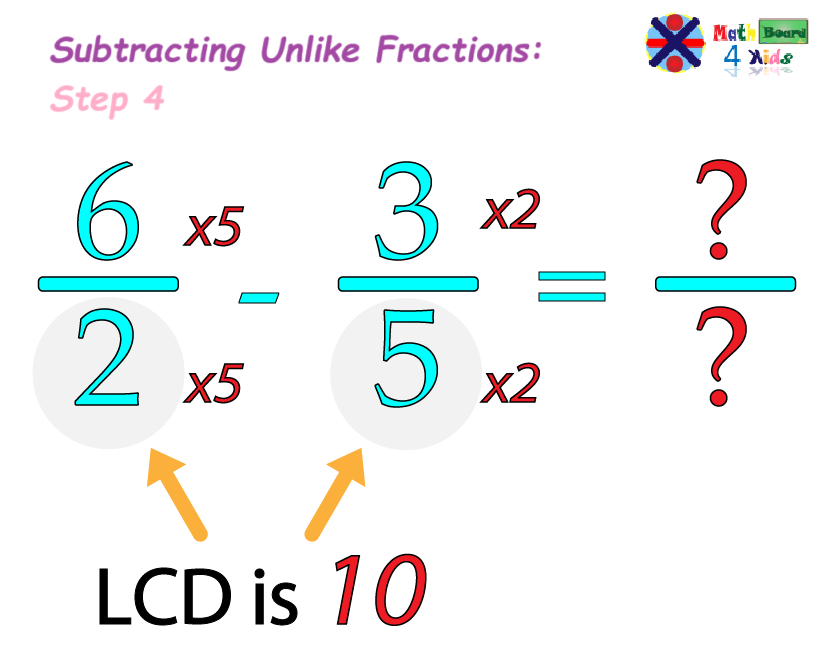
After multiplying both denominators to get the LCD and numerators to make the fractions equivalent, we can rewrite the fractions with the new numerators and denominator.
Then, we solve the fraction by subtracting the numerators and keeping the common denominator.
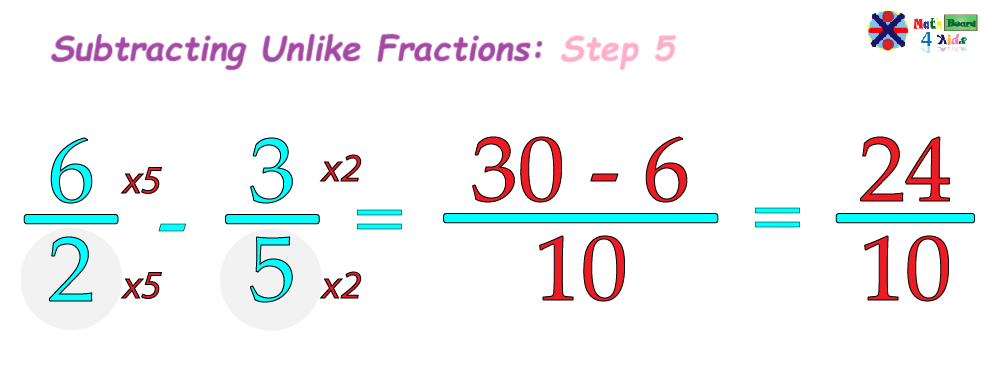
Let's remember that the Greatest Common Factor (GCF) is the largest number that can evenly divide both the numerator and denominator of a fraction. For example, in the fraction 24/10, both the numerator and the denominator can be divided by 1 and 2.
Since 2 is the larger of these two numbers, we choose 2 as the greatest common factor and divide
both the numerator and denominator by 2.
When we divide both the numerator and denominator by 2 we get 12/5.

