
Let's remember that a fraction is a way of showing sections of a whole, whether that whole consists of objects or values. It involves splitting or dividing an object or value into equal sections and showing how many of those sections are being considered or used.
Multiplying fractions is like finding a part (fraction) of a part (fraction). It’s like taking a piece of something, and then taking a smaller piece of that piece.
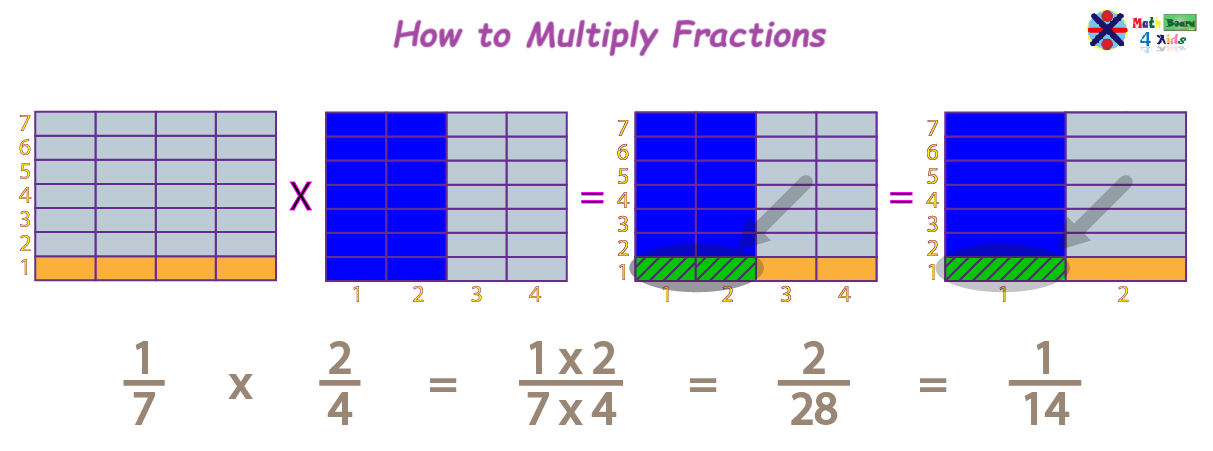
Multiplying fractions shows us how much of the whole we have when we combine two fractions. As shown in the example, the green squares represent the product of the multiplication.
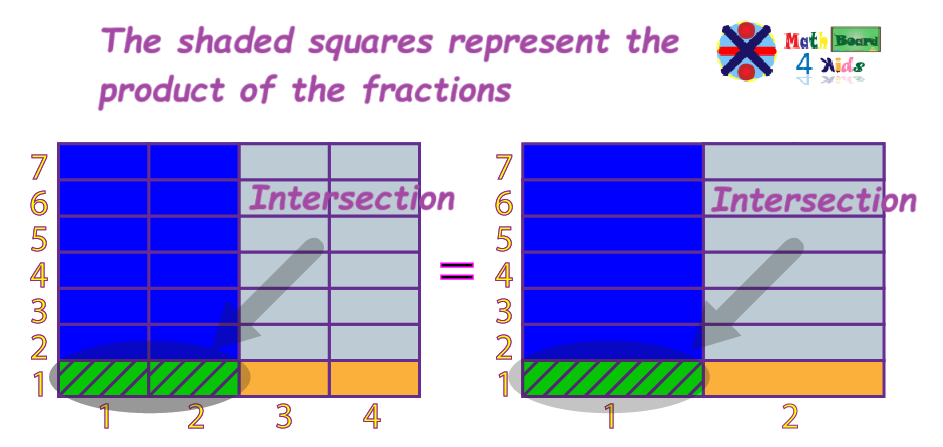
Since multiplying fractions doesn’t require both fractions to have a common denominator, we don’t need to find one. The steps are easier.
When multiplying fractions, we begin by multiplying the numerators (the top numbers of the fractions). This gives us the new numerator (top number) of the product.

Then, we multiply the denominators (the bottom numbers of the fractions). This gives us the new denominator (bottom number) of the product.

Next, we write the results or products of the multiplications for both the numerator and denominator.
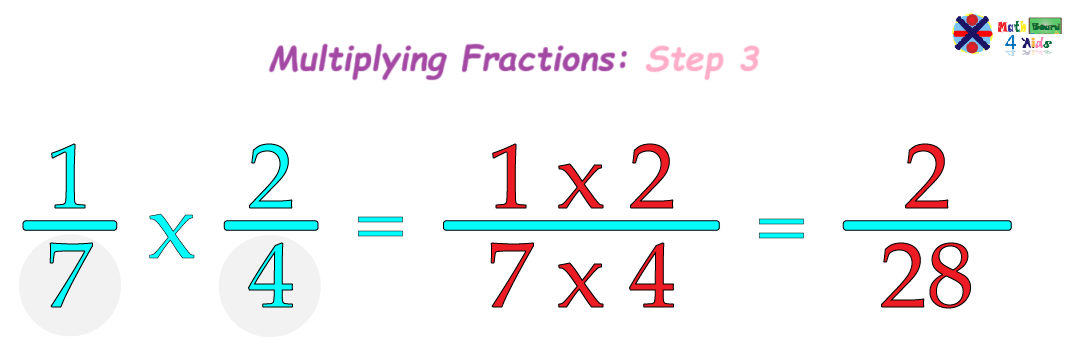
Let's remember that the Greatest Common Factor (GCF) is the largest number that can evenly divide both the numerator and denominator of a fraction. For example, in the fraction 2/28, both the numerator and the denominator can be divided by 1 and 2. Since 2 is the larger of these two numbers, we choose 2 as the greatest common factor and divide both the numerator and denominator by 2.
When we divide both the numerator and denominator by 2 we get 1/14.
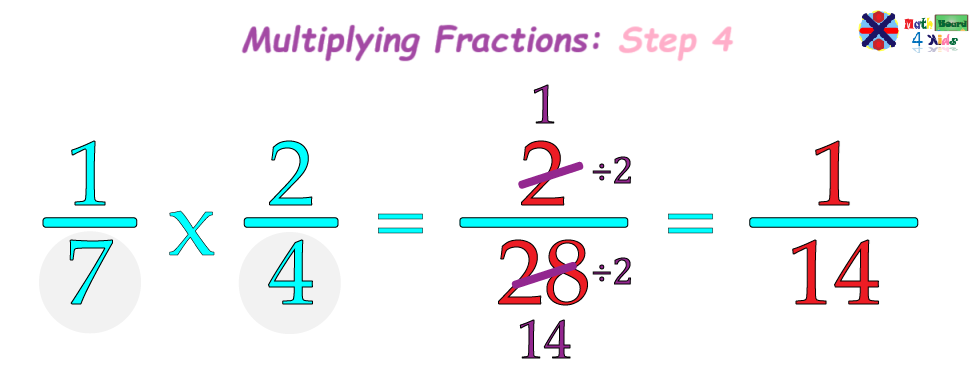
And those are the steps for multiplying fractions!